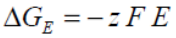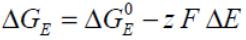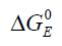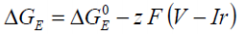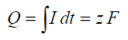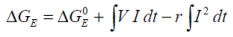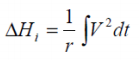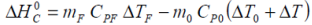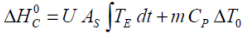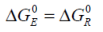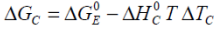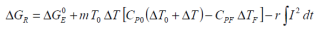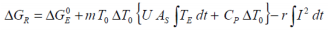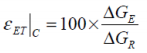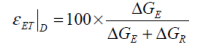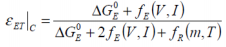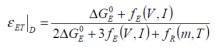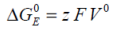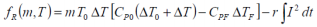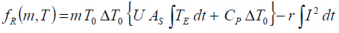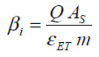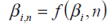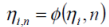Introduction

Accelerating rate calorimetry is well suited to studying both the thermokinetics and thermodynamics of chemically reactive exothermic systems. Originally developed as a tool to aid the chemical and allied industries, the technique has gained considerable popularity within the battery manufacturing community.

The THT Accelerating Rate Calorimeter has a number of options available, designed to study batteries during cycling (KSU) and abuse (BSU). The Gibbs free energy (ΔG) of a system may be determined and used as an indicator of hazard potential. Further more, changes in ΔG based on calorimetric and electrometric data may be used to study the effects of cycling on battery efficiency.

Battery Development

Energy density improvements have always been central to lithium and lithium ion battery development. In addition to this, increases in total capacity for applications such as electric vehicles (up to 30kWh) create a further cause for concern.

These issues, along with the hazardous nature of lithium itself have generated considerable concern amongst Li-ion battery manufacturers. In particular, safety awareness rises following the aftermath of a fire and/or explosion incident. Such incidents may typically occur during battery storage or transportation, and occasionally during use where exceptional circumstances (ie. conditions exceeding design) have prevailed. A greater uncertainty also exists when dealing with secondary battery types, since the effects of cycling must also be considered.

It has therefore become necessary to attempt to quantify the potential hazards that exist when handling and using Li-ion batteries. A means of assessing the thermal stability of a Li-ion battery with use and /or prolonged storage must be defined, such that a safe battery life (SBL) may be quantified.

The approach that is adopted in this paper, will address this point by considering the thermodynamics and electrodynamics of a battery, and drawing a comparison between these. A means of establishing whether or not a battery has exceeded its safe useful life may hence be defined.

The Accelerating Rate Calorimeter (ARC) provides an adiabatic environment in which a sample may be studied under conditions of negligible heat loss. The calorimeter configuration is such that the sample is suspended within an enclosed environment (a heavy duty cylinder with base and lid) whose temperature is controlled extremely precisely. Thus adiabaticity is achieved by tracking (ie. matching) the temperature of the test sample closely (usually to within less than 0.01ºC) when operating within the ARC’s dynamic range. It may further be used in an isothermal mode of operation, with tracking becoming a variable factor that may be set.

Tests conducted in the ARC provide temperature, temperature rate and pressure data as functions of time. This information may be used to study both the thermodynamics and thermokinetics of a process. In our case it is the thermodynamics that will be considered.

If we consider the work done in a reversible electrical environment, the electrical Gibbs free energy may be equated to:

...where F is the Faraday constant, z is electron moles and E is the potential difference.

Considering changes in potential difference ΔE resulting from charge / discharge operations:

Where: 

...is the standard electrical Gibbs free energy with reference to zero potential.

In reality the reversibility of the electrical work does not hold, and it is necessary to incorporate the effects of battery self heating which results in energy losses. These energy losses are seen as heat.

The thermal effects resulting from power generated due to the internal resistance of a battery may be quantified by considering:

....where V is the voltage across the battery and I the current.

Now since the transferred charge is: 

....this may be restated as 

This allows the ΔGE to be determined from electrodynamic data.

Calorimetric techniques such as those available with the ARC® are useful tools in studying the overall thermal performance of chemical reactions.

The technique therefore lends itself to studying the overall nature of an energy change in a battery if both electrokinetic and thermokinetic parameters are studied concurrently. During such a study there are two main sources of thermal energy, the first being due to the electrochemical reactions which proceed during the charging and/ or discharging processes, and the second being the heat due to a battery’s internal resistance.

This heat may expressed as: 

for a fixed internal resistance. Any internal resistance changes have to be considered over a prolonged battery usage programme. The effect is not significant over a small number of cycles (≤ 10 say), and so in this instance it can be considered a constant.

If the experimental heat generated during a charge and/or discharge cycle is considered, the standard overall heat determined adiabatically

 may be equated to.. 

In the case of isothermal conditions prevailing in the immediate environment the response differs 

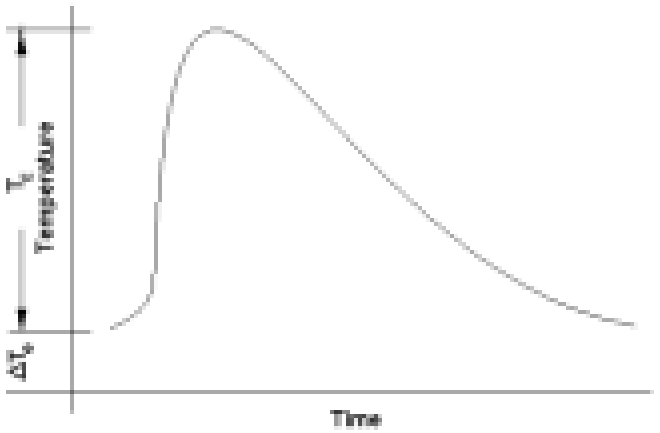
such that: 

where T E is the temperature difference with reference to the environment.

Apart from the possibility of mass loss resulting from minor gas release during charge and/or discharge, the battery mass may be considered constant such that m0 = mF. From the Van’t Hoff equations we have: 

Both electrical and thermal standard Gibbs free energies may be considered constant and represent the ideal transition from the zero potential state to the standard state by definition. Hence: 
so that restating the Van’t Hoff relationship: 
Simplifying the above for the adiabatic case, whilst removing the internal resistance effects on the calorimetric Gibbs free energy gives rise to the Gibbs free energy for the isolated electrochemical reaction: 
...with T0 the cycle start temperature. Similarly for the isothermal case at temperature T 0: 

As a battery ages with prolonged storage and repeated cycling, one may consider the available free energy function with respect to both electrical energy and thermal energy as indicators of change in preferred chemical pathways.

A direct comparison between the free energies attributed to a battery’s electrodynamics and thermodynamics may be defined as a form of Gibbs free energy characterisation.

The term free electrothermal energy characterisation (εET) is suggested, where for the charging process: 

...and for the discharge: 

This value may be perceived as an indicator of electrochemical deterioration within a cell and as a comparator with which different battery chemistries and types may be categorised.

The free electrothermal energy characterisation may be determined thus: 

..when charging, and: 
....when discharging, where: 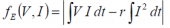              ....and: 

When considering the adiabatic case, the thermal aspect of the relationship may be expressed as: 
 

..whilst in the isothermal case: 

There is a need for identifying an overall performance factor for batteries which incorporates both the compactness of the cell as well as its thermal performance.

This latter point considers both the safety related properties of a battery as well as incorporating to a degree the overheads that will inevitably have to be addressed when considering the heat management of a battery (or battery pack). In the cases of charging and discharging, the battery performance factor (β) is given thus: 

...where i is the total cycle count, Q is the charge capacity of the battery (Ah), AS is the surface area of the cell with mass m, taking into account the characterisation and heat dissipation potential of the design. β i is determined as a function of i for a given cycling rate, C/n.

Subsequently a surface may be defined for a cell, such that: 

For instance using β i,r it is possible to compare a large 50 Ah cell with a 500 mAh cell. The cells may have either identical or dissimilar chemistries, may be prismatic or can type, jelly-roll, have a complex arrangement, etc.

It should be noted that a number of battery related criteria are omitted from the performance function β i,r . Such data is related to data obtained from the more traditional battery safety tests which stress a battery beyond its normal operation limits.

Such abusive tests are adiabatic ARC tests, hot plate tests, overcharging tests, crushing tests, piercing tests, etc. The battery performance function is therefore devised to relate batteries under non-abusive conditions, and in so doing does not conflict with data obtained from such experiments.

Finally an overall Gibbs free energy efficiency (ηET) may be defined, based on the ratio between the battery performance factors with regards to the charging and discharging processes. 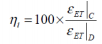       Once again an efficiency surface may be determined for different cycling rates, ie. C/n, such that: 

The ARC

The ARC is one of the most sensitive adiabatic calorimetric techniques currently available. With sensitivities of up to 0.005°C/min (typically equivalent to between 10μW/g and 15μW/g) and the ability to track to rates of up to 15°C/min, it provides a very dynamic platform for testing any sample capable of heat generation (ie. exothermic).

The ARC consists of a robust calorimeter assembly designed to contain test-cell ruptures at high temperatures and pressures.

This sits within a blast-enclosure which can contain the equivalent of a 100g of TNT detonation, and is safety interlocked during use to deny user access.

Control is achieved via the dedicated electronics units (LSU, HSU and PSU) which sit within the electronics rack along with any auxiliary options.

A user-friendly PC interface provides easy access to test setup, data logging and display as well as real time editing of test parameters during a run. The ARCCal+ analysis package provides the platform for data analysis.

Figure 1 shows the Extended Volume system and Figure 2 shows the standard system.

The instrument’s high sensitivity relies extensively on good calorimeter calibration, a sophisticated software model which quantifies the heat content of the calorimeter in real time and a very dynamic PID control algorithm.

The calibration relies on the execution of an automated procedure which is designed to account for differences in the response of the various thermocouples within the calorimeter at set temperatures. Typically the ARC® is calibrated to drift rate of ±0.01°C/min.

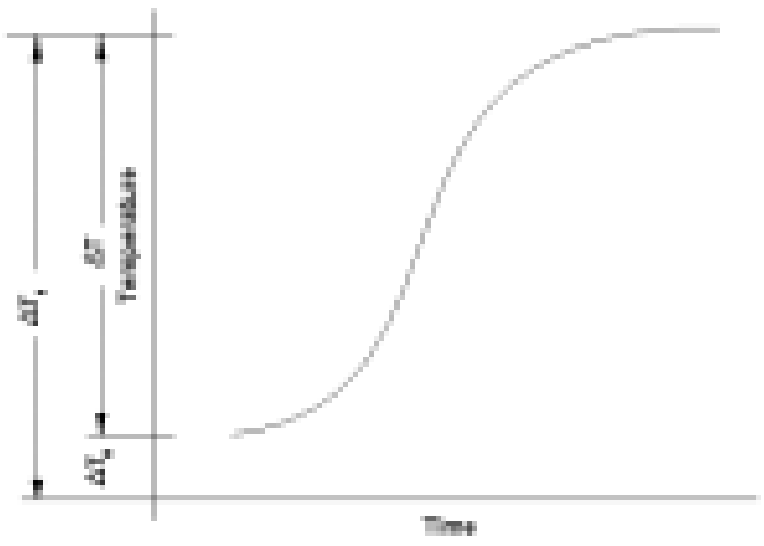
In its standard Heat-Wait-Seek (HWS) test mode, a sample is heated from a preset start temperature to an end temperature in a series of heat steps. After a heat step, the sample is allowed to reach a thermally homogeneous state during the wait phase.

Once this homogeneity is attained, an adiabatic environment is maintained through extremely precise control of the sample to calorimeter temperature difference (±0.001°C to ±0.01°C).

This is the seek phase. If exothermic activity is detected, the adiabaticity is maintained and the instrument tracks the sample temperature whilst logging it. This is referred to as the exotherm phase.

During most seek periods, sample self-heat generation is not detected. In this instance and also in the instance when exothermic self-heating falls to temperature rates below the set detection sensitivity (typically 0.02°C/min, ie. twice the value during calibration), the sample is heated to the next temperature plateau. When the test end temperature is reached the test stops and cooling is applied.

The Isothermal mode of operation is essentially an HWS mode with an extended seek phase at the start temperature, whereby the sample is maintained in an adiabatic environment with any residual instrument drift rate (usually ≤ 0.01°C/ min after a recent calibration) removed. Under such conditions, the temperature remains constant until exothermicity is detected with a drift rate below ±1.0×10-6 °C/min

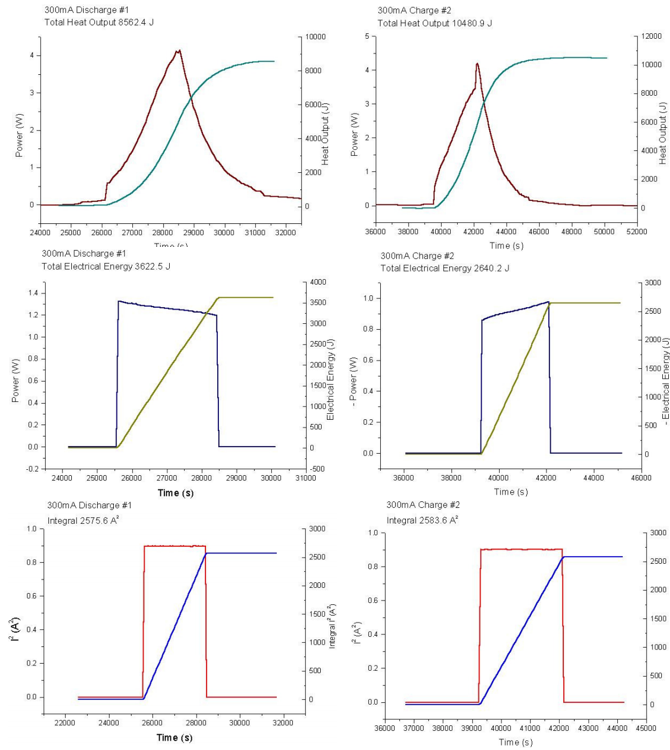
A preliminary experimental study is examined to illustrate the determination of battery performance factor.

This study used an ARC with the KSU option fitted. Tests were performed in the isothermal mode to prevent the battery temperature from 6 rising to harmful levels. A fresh 400 mAh 4/5A type secondary Li-ion battery was used with transition metal intercalated electrodes. This battery had previously been cycled only once such that changes in the battery performance factor are maximised. With an isothermal start temperature of 50°C, KSU constant current cycling at 300mA was conducted.

Preparation

During the test the battery was thermally insulated from the calorimeter environment. The ARC was running in the isothermal  mode of operation, without tracking.

Under these test conditions the calorimeter behaves like a heat sink, allowing the sample to drift above and below the calorimeter temperature. The calorimeter temperature is maintained throughout the isothermal phase, unless the temperature rate exceeds the temperature rate sensitivity threshold.

During the experiment isothermal conditions were maintained at 50°C, whilst the sample temperature was allowed to deviate.

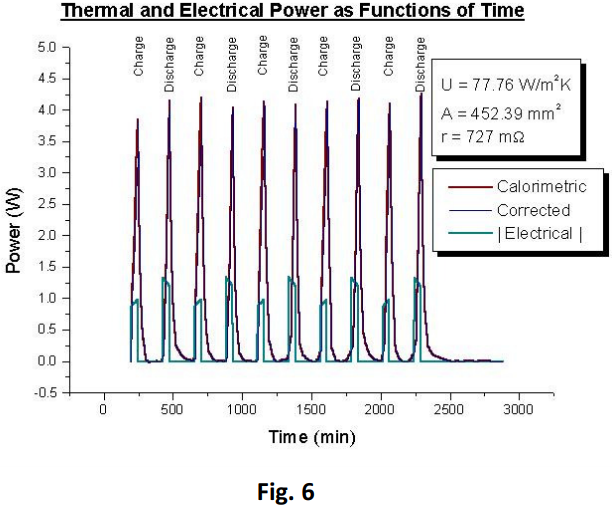
The results are displayed in a summarised form (Figure 5 & 6).

Results

The heat transfer coefficient (U) was determined directly from the cooling curve sections of the temperature-time data, which gave a time constant of τ = 704.4 s.

The heat capacity was determined calorimetrically by using the ARC® in the adiabatic mode and applying a known amount of heat (q) using a low power heater. The temperature rise (ΔTCP) gave the heat capacity as 1.26 kJ/kg K since: 
v is the voltage across the heater and i is the current. Finally, the battery surface area was determined to be 452.39 mm2 whilst its mass was 19.665 g.

Analysis

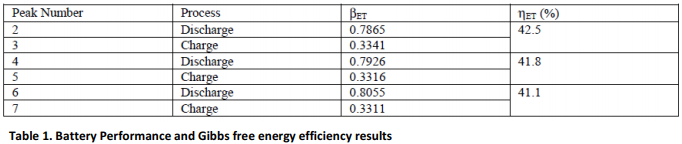
For the purpose of this analysis, peaks 2 through to 7 will be considered. Pairing 2 and 3, 4 and 5, 6 and 7, provides a basis for determining the Gibbs free energy efficiency.

In this particular case, it is evident that the Gibbs free energy efficiency drops by 0.7% per cycle. This is typical of a fresh cell (0.4% to 0.8% per cycle). Further studies would show that this value will tend to decrease with repeated cycling until an asymptotic value is established very close to zero.

Consequently the Gibbs free energy efficiency reaches a temporary minimum. This minimum value holds until the battery reaches the end of its useful life, when it drops rapidly almost to zero. We are currently investigating the effects of extensive cycling (>2000 cycles) on the Gibbs free energy efficiency.

It appears that both the battery performance factor and the Gibbs free energy efficiency may help identify a way of addressing the problems associated with heat generation during Li and Li- ion battery use. It may be possible to identify a maximum cycling count beyond which a battery’s (or battery pack’s) thermal overheads exceed its electrical performance benefits. ie. A safe battery life (SBL).

Both battery management and thermal management systems may therefore be designed to allow for this limitation. Although this may slightly reduce the acceptable lifetime of a battery, and therefore the increase costs by increasing replacement frequency, the associated hardware could as a result be designed to be both safer and cheaper.

References :

ARC Technical Information Sheet No. 067, Thermal Hazard Technology, UK

상세한 사항은 아래 첨부된 자료를 참고 부탁 드립니다.